10821. Создание двоичного дерева поиска

Бинарное дерево поиска является эффективной структурой данных для быстрого поиска. Все элементы левого поддерева меньше значения корня, а элементы правого поддерева – больше корня.

Ниже показаны деревья бинарного поиска с 4 вершинами, которые получены в результате вставки элементов порядке, приведенном под деревьями.

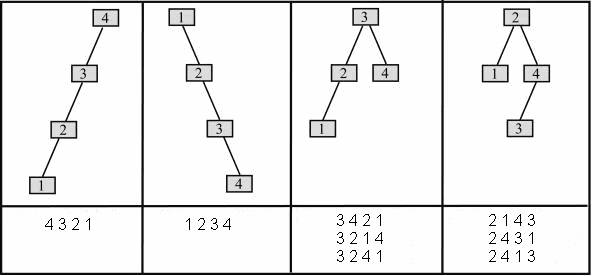
В задаче необходимо найти такой порядок вставки чисел от 1 до n в бинарное дерево поиска, чтобы получилось дерево высоты не более h. Высота дерева определяется рекурсивно:

1. Высота пустого дерева равна 0.

2. Высота дерева равна максимуму высот его поддеревьев плюс 1.

Полученный порядок должен быть лексикографически наименьшим. Например, для n = 4, h = 3 следует вывести 1 3 2 4, а не 2 1 4 3 или 3 2 1 4.

Вход. Каждая строка содержит два натуральных числа n и h (1 £ n £ 10000, 1 £ h £ 30). Последняя строка содержит n = h = 0 и не обрабатывается. Выходные данные содержат не более 30 тестов.

Выход. Для каждого теста вывести его номер и порядок вершин, в котором они будут вставляться в бинарное дерево поиска высоты не более h. Если такого дерева не существует, то вывести сообщение ‘Impossible.’.

Пример входа

4 3

4 1

6 3

0 0

Пример выхода

Case 1: 1 3 2 4

Case 2: Impossible.

Case 3: 3 1 2 5 4 6

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Полное бинарное дерево высоты h содержит 1 + 2 + 4 + … + 2^h-1 = 2^h - 1 вершин. Если n ³ 2^h, то искомого дерева не существует. Иначе будем строить такое дерево, в котором будет по максимуму заполняться правое поддерево.

Пусть следует расположить в дереве поиска высоты не более h числа от a до b. Тогда в правом поддереве высоты h – 1 следует расположить 2^h-1 – 1 элементов, а число d = b – 2^h-1 + 1 следует расположить в корне. Числа от a до d – 1 располагаем в левом поддереве. Если d < a, то в левом поддереве чисел не будет и в таком случае положим d = a.

Пример.

Рассмотрим второй пример, где n = 6, h = 3. Дерево высоты 3 может содержать до 2³ – 1 = 7 вершин. В корне дерева расположим число d = 6 – (2² – 1) = 3. Рекурсивно вставляем числа от 1 до 2 в левое поддерево и числа от 4 до 6 в правое. Получим последовательность 3 1 2 5 4 6.

Реализация алгоритма

Функция find располагает в дереве поиска высоты не более h числа от a до b и выводит их. Число d = b – 2^h-1 + 1 располагаем в корне, числа от a до d – 1 располагаем в левом поддереве, числа от d + 1 до b в правом. Если правое поддерево будет запонено не полностью, то d < a. В таком случае левое поддерево будет пустым, в корне расположим d = a, а числа от a + 1 до b вставим в правое поддерево. Обработку заканчиваем, как только правый конец интервала станет меньше левого (a > b).

void find(int a, int b, int h)

{

int d = b - (1 << (h-1)) + 1;

if (a > b) return;

if (d < a) d = a;

printf(" %d",d);

find(a,d-1,h-1);

find(d+1,b,h-1);

}

Последовательно читаем входные значения n и h, печатаем номер теста. Проверяем, существует ли искомое дерево: выводим ‘Impossible.’, если n ³ 2^h. Иначе выводим искомую последовательность вершин, вызвав функцию find(1, n, h).

while(scanf("%d %d",&n,&h), n+h)

{

printf("Case %d:",cs++);

if (n >= 1 << h) printf(" Impossible.");

else find(1,n,h);

printf("\n");

}